Moonmaker

This is a Moon-making system we devised a while ago. The goal was to produce moons similar in size and composition to the ones found in our solar system. The main challenge was how to produce the massive surfaces of these moons -and their interiors- while keeping them interesting. Also, we had to make sure these could be rendered with crisp detail regardless of how far you are from them.

The system assumes the moons have a spherical base. The system uses a geodesic meshing for the base sphere to guarantee each surface patch has the same area. The system uses this structure only as a computational grid for the procedural generation, the actual moon surface will be much smoother than the generation grid.

Geodesic sphere

For smaller, irregular moons, the base geometric definition of the moon will be perturbed by a low-frequency 3D noise.

Noise-perturbed geodesic sphere

Starting from this base, the system will use a series of concentric shells. Each cell will determine the volumetric characteristics up to the next concentric shell. The outmost shell will provide the surface properties of the moon.

Multiple concentric shells

Each shell will be optionally distorted by a low-frequency 3D noise that is unique to the shell. If configured to be so, it is possible for an inner shell to overcome an outer shell.

Shell distortion

The preceding diagrams have exaggerated the distance between shells, and the magnitude of their distortion, to provide a better understanding of this constructive process. In practice, shells will be much closer to each other, and the magnitude of their distortion will be proportionally smaller.

The following sections will describe how the outmost shell is produced. The same principles will apply to the production of the inner shells, for this reason, the definition of inner shells will not be discussed in detail.

The procedural moon system requires both a real-time component and an offline component. The real-time component will be running in the player’s computer. The offline component will run in the game developer’s computers. The offline generation component will produce information that can be quickly augmented by the real-time component.

Each vertex in a spherical shell will be classified as belonging to one specific biome. A biome is a collection of surface properties, including, but not limited to: elevation, material distribution, instance placement, and material coloration.

Example of biome

The biome information contains entropy-rich features like craters, dry seas, surface cracks due to gravitational tides.

Large crater captured in biome information

The biome definition also contains planting rules, which will determine the location, frequency, and randomization of smaller features like rocks, boulders, overhangs, etc.

Rock instances over terrain

Each biome is be made of tile-able elements so the real-time component can apply the same information in multiple locations of the moon, and in other moons as well. The biome information will also be designed in a way that fast distortion and re-combination are possible, thus reducing repetitive and predictable patterns in the environment.

The system uses two types of biome tiles: Transitional and Isolated.

Transitional biome information will appear in regions where a biome is transitioning into a neighboring biome. Isolated biome information will appear in regions the system can guarantee there are no neighboring biomes.

These two distinct modes are needed because some large biome features like craters, can only be placed in areas where the biome is not transitioning into another biome type since biome transitions can affect the height profile and overall look of the terrain features.

The following simplified example shows a moon that uses three different biomes: Polar, Tropical, and Equatorial. The biomes are colored Red, Blue, and Green respectively.

A moon with three biomes

Patches, where there is an Isolated biome, appear in a solid color, patches with Transitional biomes show a blend of colors.

The system will use a set of pre-computed noises to introduce variation in the biome transition zones, creating interesting, unique transitions from one biome into another.

Procedural noise applied to biome transitions

The preceding images have exaggerated the size of each biome patch relative to the moon’s size to provide a better understanding of the biome patching technique. A single biome patch will cover an area of approximately 10km by 10km. A moon having 1,500 km radius will have a surface area of 30,000,000 km2. To cover its surface, it would take nearly 300,000 of these patches.

Biome grid resolution for a moon of 1,500 km radius

The biome grid resolution can lead to a very large number of biome patches. The system will not keep track of these individually since each patch’s location can be analytically computed, and for most of the patches, their biome assignment can be inferred from a high-order biome map.

High-order biome maps will provide the moon’s key characteristics when viewed from far away. The system will use these maps to generate additional detail for closer views, keeping the moon’s definition consistent when viewed at different scales.

High-order biome maps are 2D images that can fit the moon’s surface using a custom 2D parametrization. Each point of the map contains a numeric identifier for the biome that is prevalent in that location of the surface or internal shell.

2D biome map

The image above shows a map with four different biome types (blue, red, yellow and white). The image is wrapped around the sphere using a custom 2D parametrization. One possible parametrization is shown below:

2D parametrization for Biome Id map

In addition to the biome Id map, the system will allow other maps. For instance, maps containing elevation and surface color.

Elevation, tint, and a far-range rendering of the moon

A single pixel in each image may cover 4 km2, making them inexpensive to produce. These elevation and tint maps can be either procedurally generated or artist-made. For a project containing only dozens of moons, and where each moon is required to have rich, unique natural properties, this is a stage where artist input is likely to yield the best returns.

The following image captures the entire approach to generating shell surface elevation and other properties:

The three scales used for moon construction

A moon will be made of at least one spherical shell. In case there are multiple shells, the system will extrude inner shells based on their maximum radius and the shell’s height function, which is obtained from the same multi-scale process described in the previous sections.

For each shell, the moon designer will provide a high-order biome distribution map, biome definitions for the biomes appearing in this map, and material definitions for the materials appearing in the biome.

The system accepts “air” as a valid material, which can be used to create cavities within any shell.

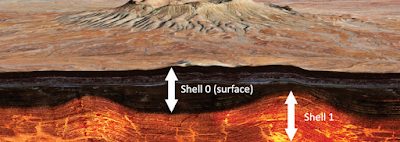
A cross-section of the moon terrain, displaying two different shells

A single shell will also be a volumetric object, and its depth will be defined by a stack of materials. The material stack information will be contained in the biome.

A material stack made of 6 materials

Since underground materials will rarely become exposed, they can be expressed at a much lower resolution than biome surface materials and the use of local procedural noises will not be noticed by the player.

The material stack functionality may be sufficient to place as some materials in the stack can be sufficiently rare. The biome designer will be able to configure the abundance and occurrence pattern of any material in the stack.

The procedural generation is executed by both GPU shaders and CPU voxel algorithms.

The shader will compute a fragment color for each of the three scales, and it will blend these samples based on the distance from the camera to the fragment.

Any detail that is small enough to not register in the geometry, but that still contributes to the perceived complexity of the surfaces, will be captured by normal maps generated in real-time from the procedural definition of materials, biomes or the high-order moon definition maps. This technique will keep low polygon counts for the scene.

The trade-off is that biome and high-order definition maps will have to be resident on GPU while the moon is in view. It is possible to selectively upload only the mipmaps necessary for rendering the current moon scale. The total amount of GPU memory required at any time will be reduced to a minimum by streaming mipmaps in and out of GPU as the viewer position changes.

When features become large enough due to their proximity to the camera, they begin to appear in the geometry output by the real-time voxel generation. This also applies to any sections of the moon that may have been terraformed or mined by the players. If the changes are large enough they could be perceived from orbit, as Voxel Farm’s adaptive scene manager will increase the LOD for any areas with modifications deemed important by the application.

Thinking about voxels

Very often people ask me what a voxel is. I struggle to explain this in simple terms, even to savvy professionals from other fields of IT. In most occasions, I just say a voxel is like a pixel, but in 3D, and move on to refresh my drink or hide in a lavatory. I can't help the feeling I have avoided the question.

To help understand why voxels matter today, we need a different analogy. If I had enough time, I would say voxels are like triangles.

A triangle defines a closed 2D space. Imagine we want to do something to this closed space, for instance, paint it red. We could do this by drawing one long line and making the right turns until we have our triangle:

This is how most triangle rasterization worked in the early days. Even after many clever optimizations, it remained awfully slow. It was an inherently serial solution. The value we paint for one point depends on computations we made for earlier points. This would never scale up to hundreds of millions of triangles per second, even with the transistor densities we have today.

GPUs changed that. They render triangles faster only because the problem is solved in parallel. Remember how a triangle is a closed 2D space? That means there is "inside" versus "outside". The GPU, with a simple test, will know this. If a point is inside it will be painted red. It does not matter whether previous points were inside. Since there are no dependencies between points, the GPU is free to look at many points at the same time.

This amazing property of triangles, where they can tell inside from outside without any additional context, enabled the GPU age.

Just like a triangle defines a closed 2D space, a voxel defines a closed 3D space. And just like a triangle, a voxel can have any properties you want. It could have a color, or a material, or even surface parametrization. Voxels can use UV maps and textures in the same way triangles do. In this next image, you can see this voxel rock that looks indistinguishable from your typical low-poly textured mesh:

We tend to think of voxels as cubes, and most of the time this is correct. A voxel cube is equivalent to a surface quad. Just like the quad can be split into two triangles, a voxel cube can be split into five tetrahedron voxels.

And just like triangles did for 2D problems, voxels enable massively parallel processing for problems in 3D. I think this is a big deal.

But what are these problems that you need to solve in 3D?

Rendering is not one of them, contrary to what intuition may tell you. Rendering is about projecting the data into 2D so humans can understand it. It will always be solved more efficiently using 2D elements like triangles and surface processors like GPUs. While "seeing" is very important for humans, it does not really mean anything to a computer. They have no problem working in higher dimensions.

Pretty much everything else is a problem in 3D. Here is a basic one: Imagine you needed to compute the volume of a very random 3D object that has the size of a small town. If you are using voxel data, you can have hundreds of nodes in a network compute a small section of the object's volume and then add the results to get the final volume. You would get the results in a fraction of the time. This is only possible because voxels, like triangles did it for GPUs, allow you to answer the inside/outside question locally. That's the voxel Eureka moment.

This enables many Holy Grail solutions which for brevity reasons I won't enumerate, but that I will be happy to discuss if you drop me a comment below.

Today, most of the entertainment and geospatial industries still use serial, on-core, approaches to solving their 3D content problems.

As the data grows and more entities are required to produce it and consume it, the shift to parallel computing will necessarily happen. And we can be certain voxels will be at the heart of this next age, just like triangles were at the center of the GPU revolution.

Back to the Farm

We have built a pretty neat system. It is a spatial storing and processing platform.

If you check the origins of this project, you'll see it was about using a server farm to store and process 3D content. This system is the realization of this early goal.

The system can store virtually unlimited data, it can cover millions of square kilometers at a sub-millimeter resolution and it can serve a virtually unlimited number of concurrent users.

As it is today, you would use it as a self-serve website, like Dropbox but for spatial data:

We can take raw data in the form of point clouds, heightmaps, imagery, meshes, etc. and convert them into more useful things like terrain surfaces or volumetric models. You can view these datasets right in the browser.

The really cool part is the parallel processing. Thanks to this aspect, we can compute complex volumetric operations and other queries on the data in real time. For instance, we can compare two different snapshots of terrain and show what has changed:

In the near future, we will link the Voxel Farm plugins for Unity and UE4 to this system, so you can easily share these datasets among team-members and even end-users.

The first release of this system will be very oriented towards the geo-spatial and mining industry, we will focus on entertainment projects a bit later.

I will be covering this in more detail in future posts, but if you are intrigued by this drop me a line to miguel at voxelfarm.com and I will send you a link.

Making the Citadel

We just put up a video of how the Magic Citadel demo for UE4 was built:

The demo is not available yet, we are still working on the game-side of it in UE4, but the Citadel model is pretty much complete at this point. I would like to cover a couple of aspects that I find interesting from this experience.

A question I often get is why use voxels at all. I usually point at the obvious bits: If you want to do real-time constructive solid geometry (CSG) pretty much anything else is too slow. CSG is what allows to create game mechanics like harvesting, tunneling, destruction and building new things. Also, if you are doing procedural generation of anything that goes beyond heightmaps, voxels make it much easier to express and realize your procedural objects into something you can render using traditional engines like UE and Unity.

What I rarely say is that once you work with voxels, your mind changes. I let people figure this out by themselves, I do not want to be that weird guy saying you really need to try LSD. You change because you begin seeing your entire project as a single fabric of content. You feel more like you are working on a canvas. There is no difference between a tower roof versus terrain you have terraformed. It is a really distinct feel, which cannot be explained rather experienced.

If you have developed for UE4 or Unity before, think of how you would approach a project like this Citadel. While it is possible, you would be building out of a myriad of objects placed in your scene. You would have an object for the terrain, static meshes for the towers, walls, even the rocks making up your cliffs would be a bunch of instanced meshes clearly intersecting each other. Simply put, there is no canvas, instead, you have a collection of things.

If you want to have large organic shapes, like a massive spiral tower that slowly unravels over hundreds of meters, you would need to carefully plan how to deal with all this unique geometry. The image below shows an example of this from the Citadel:

It gets messy. This often leads to not having unique geometry at all, as it is too much trouble. It is unfortunate. Unique geometry can take your content to a whole new level. Once you have experienced it for a while, going back to the traditional instance-based approach is immersion breaking, at least it is for me now.

When you build out of individual small pieces, even if they have LODs of their own, their agglomeration cannot be trivially condensed into single objects that will efficiently LOD. Serious consideration needs to go into which objects you use to build the world, how large they can be, how you can reuse them and create cheap variations of them. All this planning takes a lot of work and mostly, a big deal of experience.

This is why it takes a Triple-A team to produce complex scenes and rich open worlds. Even when there is plenty of very talented artists out there, the slew of tricks you need to apply remains a veiled, mysterious art. We should not need GDC talks. The current state of the industry is as if Microsoft Word would limit the kind of novel you can write with it, and only those versed in Word's options and macros were able to create compelling fiction with it.

As I see it, it is really about the "fabric" that makes the virtual world. Once it becomes an organic canvas, you can automate tricks like LODs, culling and visibility sets in simple, robust ways. Let the computer do the hacks for you.

The other advantage of developing a virtual world as it were a canvas, is that your workflow becomes closer to what you experience working in Photoshop, versus the Maya-Blender experience. This is one of my favorite bits in the video above, it starts around the 2:54 mark. The artist first defines the basic volumes and then continues to refine them. I find this very intuitive and close to how people create in pixel-based systems like Photoshop.

Talking about artists, this Citadel project was possible thanks to Ben, who became part of the Voxel Farm team early this year. The amount of work he was able to put into this Citadel is incredible, as is the quality of his work. Ben caught everyone's attention as a player-builder in Landmark, under the Ginsan alias. Here is one voxel beauty he created back then:

Screenshot from Landmark (SOE/Daybreak)

A true Renaissance man, Ben also created the superb music for the video above. He often tweets about his progress in new Voxel Farm projects, if you are curious about what he is working on, make sure to follow him https://twitter.com/adamiseve

Is voxel data bigger than polygon data

We just got some fresh measurements that I would like to share.

Voxels and polygons are alternative forms of storing and visualizing 3D information. They are pretty much equivalent in terms you could represent the same information, the key difference is there are penalties attached to each method.

For instance, if you want to change the world in real-time, like making holes, cutting pieces or merging different shapes, voxels are likely to outperform polygons. The same applies if you want to merge layers of procedural content in real time. This is fast because voxels are a much simpler representation of the content. If you were doing this with polygons, you must use more complex and slower methods.

On the other hand, polygons can represent and reproduce some surfaces more economically. This is the reason why the graphics industry adopted polygons so early.

One aspect where we can do an apple-to-apple comparison is data size. The experiment would be this: Get a fairly large scene, store it both as voxels and polygons, and see which dataset is larger. We would be measuring the final size of the package, that is, how much data you need to download to have a complete scene.

This is what we did. We used Ben's work-in-progress scene, which features a massive citadel. The following video shows a character running around this place. You do not have to watch all this to realize it is a pretty big place:

(Please ignore the rough edges in the video, this is an un-optimized test aimed to get a feeling of the scale of the place.)

Everything you see there is voxel content. There are no props or instances. This is all unique geometry, forming a watertight mesh:

Here are the core stats about the scene:

54,080,225 triangles
2,203,456,000 voxels

This is the first takeaway. It takes 2 billion voxels to represent the same content as 54 million polygons. You need 40 times more voxels than polygons.

Is the voxel dataset 40 times the size of the polygon dataset?

That, you guessed, depends on how much smaller a voxel is than a polygon, also what is the overhead in storing them. Let's talk about that.

We store meshes as:

• a list of vertex coordinates (3 x 32bit float)
• a list of faces, where each face is three indices into the vertex list (3 x 32bit int)
• a list of UV pairs, one per each vertex in a face (2 x 32bit float)
• a list of material identifiers, one per each face (16 bit)

For the entire scene, the final compressed version of this data is 527 MB.

Voxels, on the other hand, store:

• attributes (empty, has material, has UV, etc. 8bit int)
• one 3D point (3 x 8bit float)
• up to 12 UV entries with surface properties (each 64bit)
• inner material (16bit int)

The compressed final version of the voxel data is 1,210 MB.

It seems the voxel data takes twice the space. This somehow feels right, considering everything we have heard about voxels versus polygons, it is no surprise voxels take twice the space as polygons for the same content.

But there is a little problem with this test. It is not really apples-to-apples. Here is why:

The polygon version of the content captures only the visible surfaces. That is when the solid materials meet air. These are the portions of the model you can actually see.

The voxel version of the content also captures hidden surfaces. While you cannot see these initially, they may become exposed later due to changes made by the viewer to the scene, for instance, while destroying or building things.

This image shows why these two sets of surfaces are different:

The red arrows point to surfaces that appear in the voxel set but are not included in the polygon set.

Luckily for us, we can change the contour rules and also produce these surfaces in the polygon dataset. After a collecting a new set of stats for this new configuration, the new polygon count is 122,470,300 triangles. Once this is compressed, the final storage is 1,105 MB.

Now, this has come very close to the voxel database size. Does this make any sense?

What is maybe most surprising is that we expected the sizes to be different. In both cases, we are capturing surfaces. Even if they are fully volumetric, voxels only really get "busy" around surfaces. This is not much different than polygons.

Of course, there are nuances in how the information is compressed. In each case, we could be using tailored compression schemes. But at this point, this will be producing diminishing returns, and the ratio between voxel data and polygon data is not likely to change much.

If you have questions or opinions about these measurements, I'd love to discuss them. Just post a comment below.